Scaling properties of stretching ridges in a crumpled elastic sheet
Alex Lobkovsky, James Franck Institute, University of Chicago,
Chicago IL 60637.
Sharon Gentges
Hao Li, Present address: NEC Research Institute, 4
Independence Way, Princeton, NJ 08540
David Morse, Institute for Theoretical Physics, University of
California, Santa Barbara CA 93106.
T.A. Witten
ABSTRACT of paper accepted in Science 9/95
Strong deformation of a sheet of solid material often leads to a crumpled
state having sharp points of high curvature. A scaling
property governing the crumpled state has been numerically demonstrated
by
examining the {\it ridges} joining pairs of sharp points in a range of
simple
geometries of variable size. As the linear size $X$ increases sufficiently,
the
deformation energy grows as
$X^{1/3}$. Remarkably, it consists of similar amounts of bending and
stretching
energy. This energy becomes concentrated in a fraction of the sheet
that decreases as
$X^{-1/3}$. Despite this concentration, the local strain in the ridge
decreases,
as
$X^{-2/3}$. Nearly all the deformation energy in thin, crumpled elastic
sheets
should be concentrated in ridges that obey these scaling laws.
-
 Energy distribution in a numerically-modeled, flat sheet of elastic material
from which two 60-degree wedges were cut. The cut edges were then joined to
form a boat shape showing a ridge singularity. Distance between vertices is
1377 times the thickness. Color indicates ratio of stretching to bending
energy. Near the vertices bending energy is more than ten times stretching
energy. In the middle of the ridge bending energy is 4.9 times stretching
energy. Alternating color stripes flanking the ridge are caused by the
vanishing of first stretching energy, then bending energy as one moves away
from the ridge. Faint induced ridges extend from each vertex and meet at
the edges at front and back. Similar ridge structures occur when a sheet or
membrane is crumpled.
Energy distribution in a numerically-modeled, flat sheet of elastic material
from which two 60-degree wedges were cut. The cut edges were then joined to
form a boat shape showing a ridge singularity. Distance between vertices is
1377 times the thickness. Color indicates ratio of stretching to bending
energy. Near the vertices bending energy is more than ten times stretching
energy. In the middle of the ridge bending energy is 4.9 times stretching
energy. Alternating color stripes flanking the ridge are caused by the
vanishing of first stretching energy, then bending energy as one moves away
from the ridge. Faint induced ridges extend from each vertex and meet at
the edges at front and back. Similar ridge structures occur when a sheet or
membrane is crumpled.
-
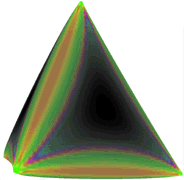 Energy distribution in a thin, flat, sheet of elastic material, cut and
joined to form a tetrahedron, showing ridge singularities. Distance between
vertices is 1581 times the thickness. Color indicates ratio of stretching to
bending energy. Near the vertices, bending energy is more than ten times
stretching energy. In the middle of the ridge bending energy is 2.95 times
stretching energy. Brightness indicates total energy density. Alternating
color stripes flanking the ridges are caused by the vanishing of first
stretching, then bending energy as one moves away from the ridge. Similar
ridge structures occur when a sheet or membrane is crumpled. Colored
patches in the faces near each vertex are artifacts from the lattice used to
simulate the sheet.
Energy distribution in a thin, flat, sheet of elastic material, cut and
joined to form a tetrahedron, showing ridge singularities. Distance between
vertices is 1581 times the thickness. Color indicates ratio of stretching to
bending energy. Near the vertices, bending energy is more than ten times
stretching energy. In the middle of the ridge bending energy is 2.95 times
stretching energy. Brightness indicates total energy density. Alternating
color stripes flanking the ridges are caused by the vanishing of first
stretching, then bending energy as one moves away from the ridge. Similar
ridge structures occur when a sheet or membrane is crumpled. Colored
patches in the faces near each vertex are artifacts from the lattice used to
simulate the sheet.
-
Stretching-energy profile of tetrahedron.
Darkness is stretching energy density
University of Chicago Materials
Center
 Energy distribution in a numerically-modeled, flat sheet of elastic material
from which two 60-degree wedges were cut. The cut edges were then joined to
form a boat shape showing a ridge singularity. Distance between vertices is
1377 times the thickness. Color indicates ratio of stretching to bending
energy. Near the vertices bending energy is more than ten times stretching
energy. In the middle of the ridge bending energy is 4.9 times stretching
energy. Alternating color stripes flanking the ridge are caused by the
vanishing of first stretching energy, then bending energy as one moves away
from the ridge. Faint induced ridges extend from each vertex and meet at
the edges at front and back. Similar ridge structures occur when a sheet or
membrane is crumpled.
Energy distribution in a numerically-modeled, flat sheet of elastic material
from which two 60-degree wedges were cut. The cut edges were then joined to
form a boat shape showing a ridge singularity. Distance between vertices is
1377 times the thickness. Color indicates ratio of stretching to bending
energy. Near the vertices bending energy is more than ten times stretching
energy. In the middle of the ridge bending energy is 4.9 times stretching
energy. Alternating color stripes flanking the ridge are caused by the
vanishing of first stretching energy, then bending energy as one moves away
from the ridge. Faint induced ridges extend from each vertex and meet at
the edges at front and back. Similar ridge structures occur when a sheet or
membrane is crumpled.
 Energy distribution in a thin, flat, sheet of elastic material, cut and
joined to form a tetrahedron, showing ridge singularities. Distance between
vertices is 1581 times the thickness. Color indicates ratio of stretching to
bending energy. Near the vertices, bending energy is more than ten times
stretching energy. In the middle of the ridge bending energy is 2.95 times
stretching energy. Brightness indicates total energy density. Alternating
color stripes flanking the ridges are caused by the vanishing of first
stretching, then bending energy as one moves away from the ridge. Similar
ridge structures occur when a sheet or membrane is crumpled. Colored
patches in the faces near each vertex are artifacts from the lattice used to
simulate the sheet.
Energy distribution in a thin, flat, sheet of elastic material, cut and
joined to form a tetrahedron, showing ridge singularities. Distance between
vertices is 1581 times the thickness. Color indicates ratio of stretching to
bending energy. Near the vertices, bending energy is more than ten times
stretching energy. In the middle of the ridge bending energy is 2.95 times
stretching energy. Brightness indicates total energy density. Alternating
color stripes flanking the ridges are caused by the vanishing of first
stretching, then bending energy as one moves away from the ridge. Similar
ridge structures occur when a sheet or membrane is crumpled. Colored
patches in the faces near each vertex are artifacts from the lattice used to
simulate the sheet.