Physical Review E 18 October 2022, 10 pages, 5 Figures
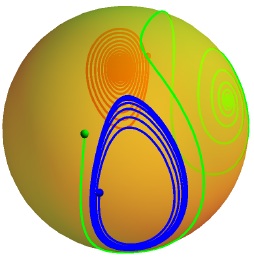
Random perturbations applied in tandem to an ensemble of oscillating objects can synchronize their motion. We study multiple copies of an arbitrary dynamical system in a stable limit cycle, described via a standard phase reduction picture. The copies differ only in their arbitrary phases $\phi$. Weak, randomly-timed external impulses applied to all the copies can synchronize these phases over time. Beyond a threshold strength there is no such convergence to a common phase. Instead, the synchronization becomes erratic: successive impulses produce stochastic fluctuations in the phase distribution $q(\phi)$, ranging from near-perfect to near-random synchronization. Here we show that the sampled entropies of these phase distributions themselves form a steady-state ensemble, whose average can be made arbitrarily negative by tuning the impulse strength. A random-walk description of the entropy's evolution accounts for the observed exponential distribution of entropies and for the stochastic synchronization phenomenon. accepted version 10 megabytes

Reports of Progress in Physics 7 October 2020, 60 pages, 17 Figures
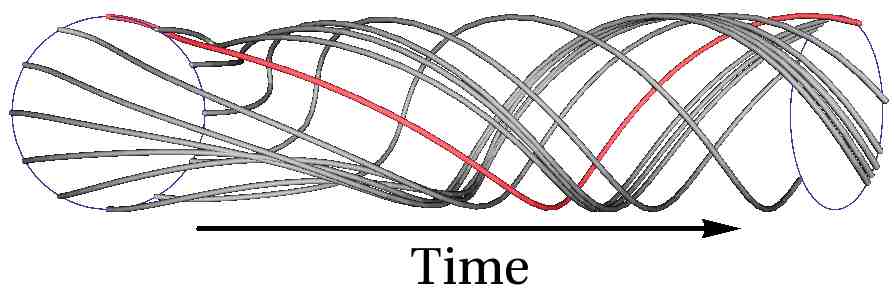
This review treats asymmetric colloidal particles moving through their host fluid under the action of some form of propulsion. The propulsion can come from an external body force or from external shear flow. It may also come from externally-induced stresses at the surface, arising from imposed chemical, thermal or electrical gradients. The resulting motion arises jointly from the driven particle and the displaced fluid. If the objects are asymmetric, every aspect of their motion and interaction depends on the orientation of the objects. This orientation in turn changes in response to the driving. The objects' shape can thus lead to a range of emergent anisotropic and chiral motion not possible with isotropic spherical particles. We first consider what aspects of a body's asymmetry can affect its drift through a fluid, especially chiral motion. We next discuss driving by injecting external force or torque into the particles. Then we consider driving without injecting force or torque. This includes driving by shear flow and driving by surface stresses, such as electrophoresis. We consider how time-dependent driving can induce collective orientational order and coherent motion. We show how a given particle shape can be represented using an assembly of point forces called a Stokeslet object. We next consider the interactions between anisotropic propelled particles, the symmetries governing the interactions, and the possibility of bound pairs of particles. Finally we show how the collective hydrodynamics of a suspension can be qualitatively altered by the particles' shapes. The asymmetric responses discussed here are broadly relevant also for swimming propulsion of active micron-scale objects such as microorganisms.
Physical Review E. accepted 12May 2020 accepted version (.pdf 4MB)
Asymmetrically charged, nonspherical colloidal particles in general perform complex rotations and oblique motions under an electric field. The interplay of electrostatic and hydrodynamic forces complicate the prediction of these motions. We demonstrate a method of calculating the body tensors that dictate translational and rotational velocity vectors arising from an external electric field. We treat insulating, rigid bodies in the linear-response regime, with indefinitely small electrostatic screening length. The method represents the body as an assembly of point sources of both hydrodynamic drag and surface electric field. We demonstrate agreement with predicted electrophoretic mobility to within a few percent for several shapes with uniform and nonuniform charge. We demonstrate strong chiral twisting motions for colloidal bodies of symmetrical realistic shapes. The method applies more generally to active colloidal swimmers.
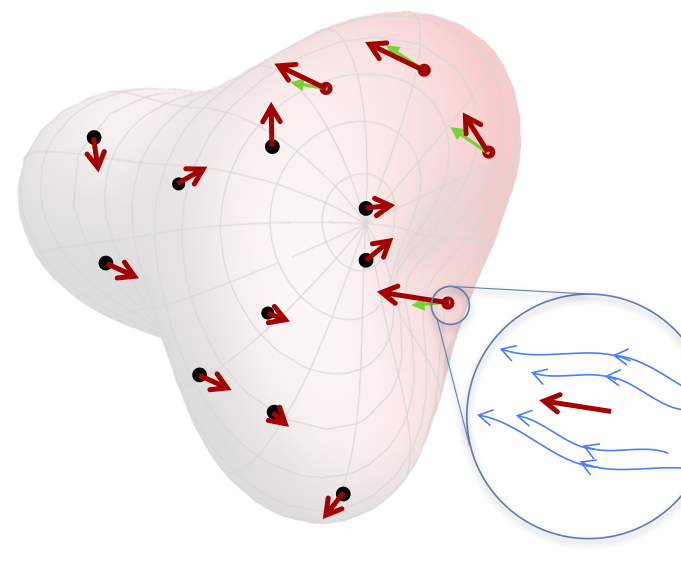
Self-propelled colloidal swimmers move by pushing the adjacent fluid backwards. The resulting motion of an asymmetric body depends on the profile of pushing velocity over its surface. We describe a method of predicting the motion arising from arbitrary velocity profiles over a given body shape, using a discrete-source "stokeslet" representation. The net velocity and angular velocity is a sum of contributions from each point on the surface. The contributions from a given point depend only on the shape. We give a numerical method to find these contributions in terms of the stokeslet positions defining the shape. Each contribution is determined by linear operations on the Oseen interaction matrix between pairs of stokeslets. We first adapt the Lorentz Reciprocal Theorem to discrete sources. We then use the theorem to implement the method of Teubner[1] to determine electrophoretic mobilities of nonuniformly charged bodies.
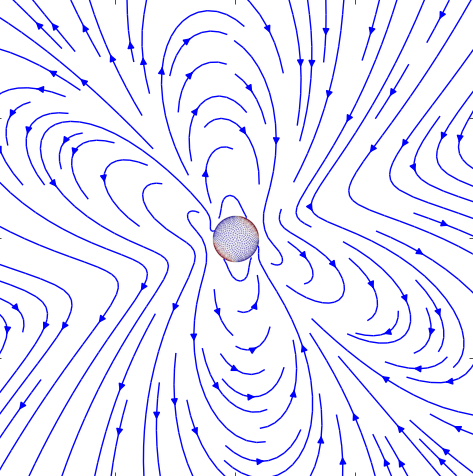
Physical Review E. 96 062613 (2017)
We formulate a numerical method for predicting the tensorial linear response of a rigid, asymmetrically charged body to an applied electric field. This prediction requires calculating the response of the fluid to the Stokes drag forces on the moving body and on the countercharges near its surface. To determine the fluid's motion, we represent both the body and the countercharges using many point sources of drag known as stokeslets. Finding the correct flow field amounts to finding the set of drag forces on the stokeslets that is consistent with the relative velocities experienced by each stokeslet. The method rigorously satisfies the condition that the object moves with no transfer of momentum to the fluid. We demonstrate that a sphere represented by 1999 well-separated stokeslets on its surface produces flow and drag force like a solid sphere to one-percent accuracy. We show that a uniformly-charged sphere with 3998 body and countercharge stokeslets obeys the Smoluchowski prediction \cite{Morrison} for electrophoretic mobility when the countercharges lie close to the sphere. Spheres with dipolar and quadrupolar charge distributions rotate and translate as predicted analytically to four percent accuracy or better. We describe how the method can treat general asymmetric shapes and charge distributions. This method offers promise as a way to characterize and manipulate asymmetrically charged colloid-scale objects from biology (e.g. viruses) and technology (e.g. self-assembled clusters).
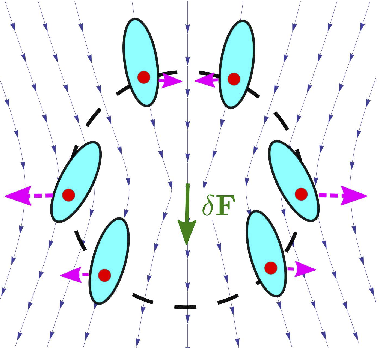
Accepted in Phys. Rev. Lett 23Mar 2017 ,
Abstract:We study the overdamped sedimentation of non-Brownian objects of irregular shape using fluctuating hydrodynamics. The anisotropic response of the objects to flow, caused by their tendency to align with gravity, directly suppresses concentration and velocity fluctuations. This allows the suspension to avoid the anomalous fluctuations predicted for suspensions of symmetric spheroids. The suppression of concentration fluctuations leads to a correlated, hyperuniform structure. For certain object shapes, the anisotropic response may act in the opposite direction, destabilizing uniform sedimentation.
Swirling a liquid from within
-
Pouring a powder into a glass of water sets off a swirling motion as the powder grains settle under gravity. The heavy grains entrain water as they drift down, dragging one another into chaotic motion. Even a uniformly stirred, resting liquid starts to swirl as gravity begins to act. Now scientists in Israel and the US have identified a way to control this swirling by adding shaped particles to the powder. They found shapes that reduce the swirling and shapes that enhance it. The shaped particles work by gliding sideways as they fall, thus reducing or increasing the slight variations of weight that cause the swirling. Industrial reactors use suspended powders to clean up water and promote chemical reactions. Shaped powders give engineers a new handle to improve the performance of these reactors.
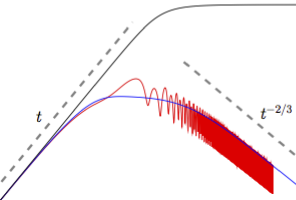
(Submitted to Phys. Rev. E on 30 Nov 2015) ,
Abstract: We study the relative translation of two arbitrarily shaped objects, caused by their hydrodynamic interaction as they are forced through a viscous fluid in the limit of zero Reynolds number. It is well known that in the case of two rigid spheres in an unbounded fluid, the hydrodynamic interaction does not produce relative translation. More generally such an effective pair-interaction vanishes in configurations with spatial inversion symmetry, for example, an enantiomeric pair of arbitrary shape does not develop relative translation instantaneously. We show that the breaking of inversion symmetry by boundaries of the system accounts for the interactions between two spheres in confined geometries, as observed in experiments. The same general principle also provides new predictions for interactions in other object configurations near obstacles. We examine the time-dependent relative translation of two self-aligning objects, extending the numerical analysis of our preceding publication [Goldfriend, Diamant and Witten, arXiv:1502.00221 (2015)]. The interplay between the orientational interaction and the translational one, in most cases, leads over time to repulsion between the two objects. The repulsion is qualitatively different for self-aligning objects compared to the more symmetric case of uniform prolate spheroids. The separation between the two objects increases with time t as t1/3 in the former case, and more strongly, as t, in the latter.
(Submitted on 1 Feb 2015) J. Fluid. Mech. accepted 13Nov 2015,
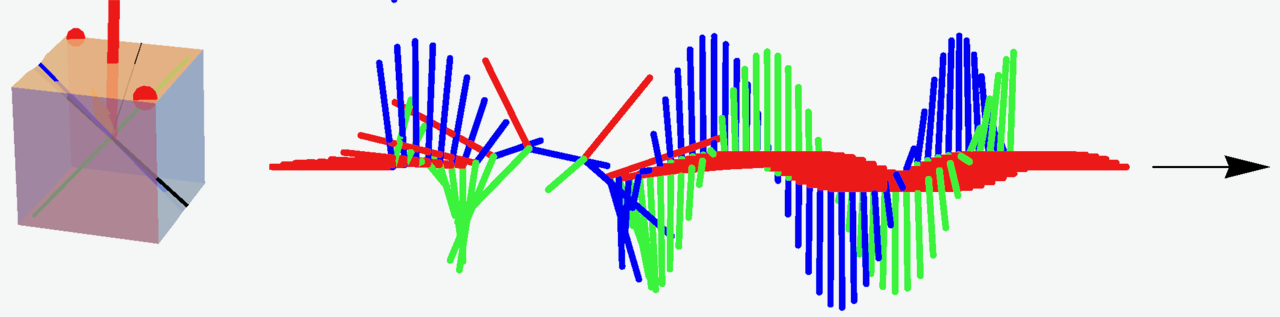
Abstract: We study the properties and symmetries governing the hydrodynamic interaction between two identical, arbitrarily shaped objects, driven through a viscous fluid. We treat analytically the leading (dipolar) terms of the pair-mobility matrix, affecting the instantaneous relative linear and angular velocities of the two objects at large separation. We find that the ability to align asymmetric objects by an external time-dependent drive [Moths and Witten, Phys. Rev. Lett. 110, 028301 (2013)] is degraded by the hydrodynamic interaction. The effects of hydrodynamic interactions are explicitly demonstrated through numerically calculated time-dependent trajectories of model alignable objects composed of four stokeslets. In addition to the orientational effect, we find that the two objects generally repel each other, thus restoring full alignment at long times.21 pages, 7 figures