\(\tilde\sigma = 1.0\) (zoomable)

\(\tilde\sigma = 1.1\) (zoomable)
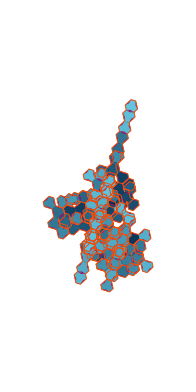
\(\tilde\sigma = 1.2\) (zoomable)

\(\tilde\sigma = 1.3\) (zoomable)

\(\tilde\sigma = 1.4\) (zoomable)

\(\tilde\sigma = 1.5\) (zoomable)

\(\tilde\sigma = 1.6\) (zoomable)

\(\tilde\sigma = 1.7\) (zoomable)

\(\tilde\sigma = 1.8\) (zoomable)

\(\tilde\sigma = 1.9\) (zoomable)
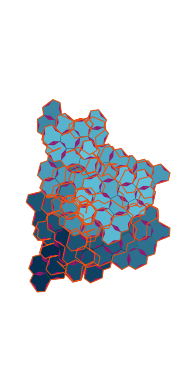
\(\tilde\sigma = 2.0\) (zoomable)

\(\tilde\sigma = 2.1\) (zoomable)

\(\tilde\sigma = 2.2\) (zoomable)

\(\tilde\sigma = 2.3\) (zoomable)

\(\tilde\sigma = 2.4\) (zoomable)

\(\tilde\sigma = 2.5\) (zoomable)

\(\tilde\sigma = 2.6\) (zoomable)

\(\tilde\sigma = 2.7\) (zoomable)

\(\tilde\sigma = 2.8\) (zoomable)

\(\tilde\sigma = 2.9\) (zoomable)

\(\tilde\sigma = 1.0\) (zoomable)

\(\tilde\sigma = 1.1\) (zoomable)
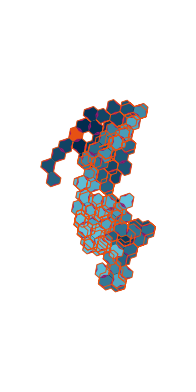
\(\tilde\sigma = 1.2\) (zoomable)

\(\tilde\sigma = 1.3\) (zoomable)
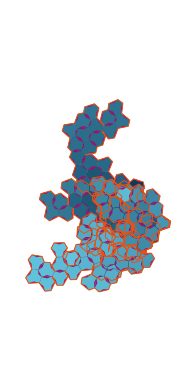
\(\tilde\sigma = 1.4\) (zoomable)

\(\tilde\sigma = 1.5\) (zoomable)
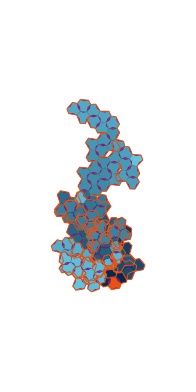
\(\tilde\sigma = 1.6\) (zoomable)

\(\tilde\sigma = 1.7\) (zoomable)
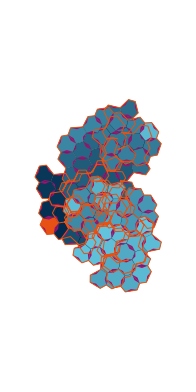
\(\tilde\sigma = 1.8\) (zoomable)
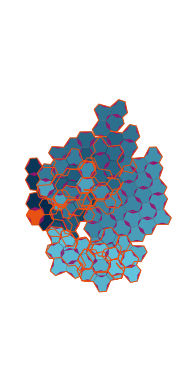
\(\tilde\sigma = 1.9\) (zoomable)
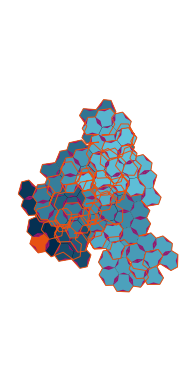
\(\tilde\sigma = 2.0\) (zoomable)

\(\tilde\sigma = 2.1\) (zoomable)

\(\tilde\sigma = 2.2\) (zoomable)

\(\tilde\sigma = 2.3\) (zoomable)

\(\tilde\sigma = 2.4\) (zoomable)

\(\tilde\sigma = 2.5\) (zoomable)

\(\tilde\sigma = 2.6\) (zoomable)

\(\tilde\sigma = 2.7\) (zoomable)

\(\tilde\sigma = 2.8\) (zoomable)

\(\tilde\sigma = 2.9\) (zoomable)

\(\tilde\sigma = 1.0\) (zoomable)

\(\tilde\sigma = 1.1\) (zoomable)

\(\tilde\sigma = 1.2\) (zoomable)

\(\tilde\sigma = 1.3\) (zoomable)

\(\tilde\sigma = 1.4\) (zoomable)

\(\tilde\sigma = 1.5\) (zoomable)
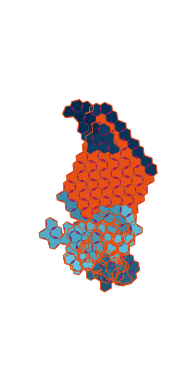
\(\tilde\sigma = 1.6\) (zoomable)
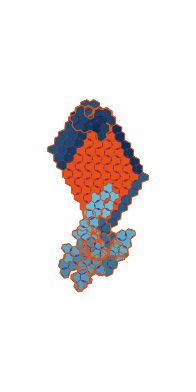
\(\tilde\sigma = 1.7\) (zoomable)

\(\tilde\sigma = 1.8\) (zoomable)

\(\tilde\sigma = 1.9\) (zoomable)

\(\tilde\sigma = 2.0\) (zoomable)

\(\tilde\sigma = 2.1\) (zoomable)

\(\tilde\sigma = 2.2\) (zoomable)

\(\tilde\sigma = 2.3\) (zoomable)

\(\tilde\sigma = 2.4\) (zoomable)

\(\tilde\sigma = 2.5\) (zoomable)

\(\tilde\sigma = 2.6\) (zoomable)

\(\tilde\sigma = 2.7\) (zoomable)

\(\tilde\sigma = 2.8\) (zoomable)

\(\tilde\sigma = 2.9\) (zoomable)

\(\tilde\sigma = 1.0\) (zoomable)

\(\tilde\sigma = 1.1\) (zoomable)

\(\tilde\sigma = 1.2\) (zoomable)

\(\tilde\sigma = 1.3\) (zoomable)

\(\tilde\sigma = 1.4\) (zoomable)

\(\tilde\sigma = 1.5\) (zoomable)
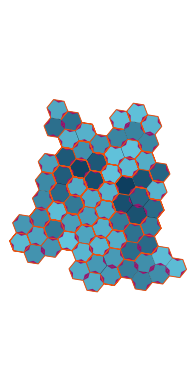
\(\tilde\sigma = 1.6\) (zoomable)
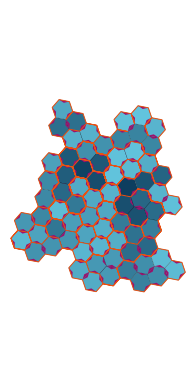
\(\tilde\sigma = 1.7\) (zoomable)

\(\tilde\sigma = 1.8\) (zoomable)

\(\tilde\sigma = 1.9\) (zoomable)

\(\tilde\sigma = 2.0\) (zoomable)

\(\tilde\sigma = 2.1\) (zoomable)

\(\tilde\sigma = 2.2\) (zoomable)

\(\tilde\sigma = 2.3\) (zoomable)

\(\tilde\sigma = 2.4\) (zoomable)

\(\tilde\sigma = 2.5\) (zoomable)

\(\tilde\sigma = 2.6\) (zoomable)

\(\tilde\sigma = 2.7\) (zoomable)

\(\tilde\sigma = 2.8\) (zoomable)

\(\tilde\sigma = 2.9\) (zoomable)

\(\tilde\sigma = 1.0\) (zoomable)

\(\tilde\sigma = 1.1\) (zoomable)

\(\tilde\sigma = 1.2\) (zoomable)
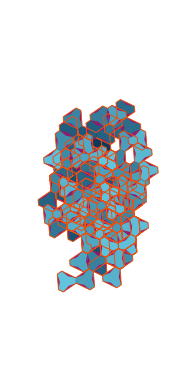
\(\tilde\sigma = 1.3\) (zoomable)

\(\tilde\sigma = 1.4\) (zoomable)

\(\tilde\sigma = 1.5\) (zoomable)

\(\tilde\sigma = 1.6\) (zoomable)
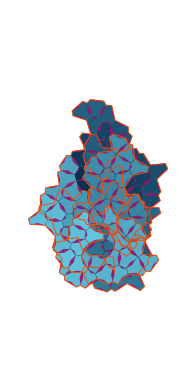
\(\tilde\sigma = 1.7\) (zoomable)

\(\tilde\sigma = 1.8\) (zoomable)

\(\tilde\sigma = 1.9\) (zoomable)

\(\tilde\sigma = 2.0\) (zoomable)

\(\tilde\sigma = 2.1\) (zoomable)

\(\tilde\sigma = 2.2\) (zoomable)

\(\tilde\sigma = 2.3\) (zoomable)
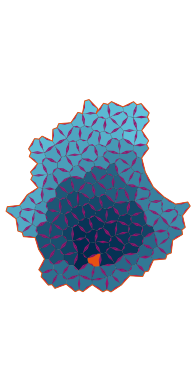
\(\tilde\sigma = 2.4\) (zoomable)
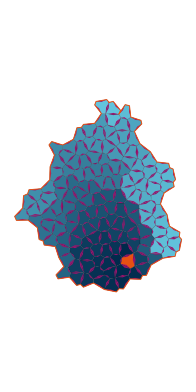
\(\tilde\sigma = 2.5\) (zoomable)

\(\tilde\sigma = 2.6\) (zoomable)

\(\tilde\sigma = 2.7\) (zoomable)
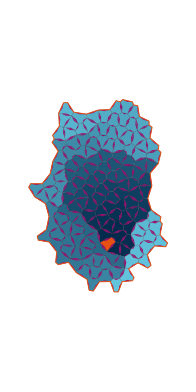
\(\tilde\sigma = 2.8\) (zoomable)

\(\tilde\sigma = 2.9\) (zoomable)
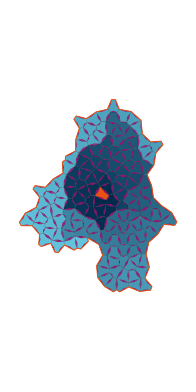
\(\tilde\sigma = 1.0\) (zoomable)

\(\tilde\sigma = 1.1\) (zoomable)
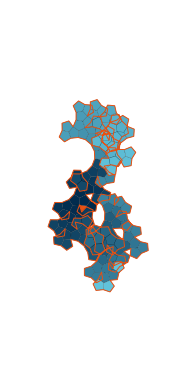
\(\tilde\sigma = 1.2\) (zoomable)

\(\tilde\sigma = 1.3\) (zoomable)
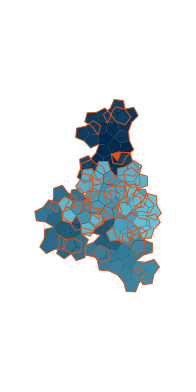
\(\tilde\sigma = 1.4\) (zoomable)
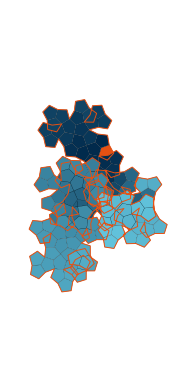
\(\tilde\sigma = 1.5\) (zoomable)

\(\tilde\sigma = 1.6\) (zoomable)

\(\tilde\sigma = 1.7\) (zoomable)
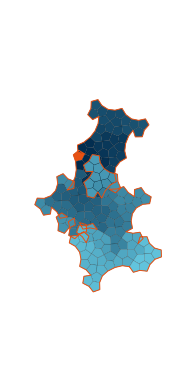
\(\tilde\sigma = 1.8\) (zoomable)

\(\tilde\sigma = 1.9\) (zoomable)

\(\tilde\sigma = 2.0\) (zoomable)
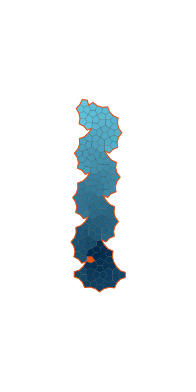
\(\tilde\sigma = 2.1\) (zoomable)

\(\tilde\sigma = 2.2\) (zoomable)
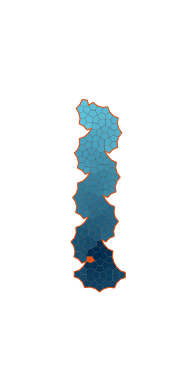
\(\tilde\sigma = 2.3\) (zoomable)

\(\tilde\sigma = 2.4\) (zoomable)

\(\tilde\sigma = 2.5\) (zoomable)

\(\tilde\sigma = 2.6\) (zoomable)

\(\tilde\sigma = 2.7\) (zoomable)
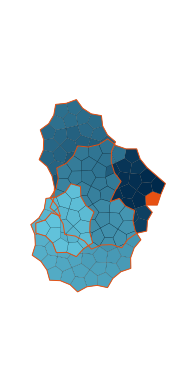
\(\tilde\sigma = 2.8\) (zoomable)

\(\tilde\sigma = 2.9\) (zoomable)

\(\tilde\sigma = 1.0\) (zoomable)

\(\tilde\sigma = 1.1\) (zoomable)

\(\tilde\sigma = 1.2\) (zoomable)

\(\tilde\sigma = 1.3\) (zoomable)

\(\tilde\sigma = 1.4\) (zoomable)

\(\tilde\sigma = 1.5\) (zoomable)

\(\tilde\sigma = 1.6\) (zoomable)

\(\tilde\sigma = 1.7\) (zoomable)

\(\tilde\sigma = 1.8\) (zoomable)

\(\tilde\sigma = 1.9\) (zoomable)

\(\tilde\sigma = 2.0\) (zoomable)

\(\tilde\sigma = 2.1\) (zoomable)

\(\tilde\sigma = 2.2\) (zoomable)

\(\tilde\sigma = 2.3\) (zoomable)

\(\tilde\sigma = 2.4\) (zoomable)

\(\tilde\sigma = 2.5\) (zoomable)

\(\tilde\sigma = 2.6\) (zoomable)

\(\tilde\sigma = 2.7\) (zoomable)

\(\tilde\sigma = 2.8\) (zoomable)

\(\tilde\sigma = 2.9\) (zoomable)

\(\tilde\sigma = 1.0\) (zoomable)

\(\tilde\sigma = 1.1\) (zoomable)

\(\tilde\sigma = 1.2\) (zoomable)
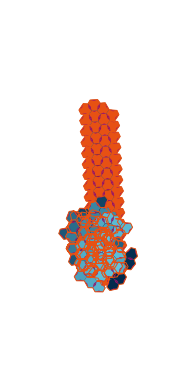
\(\tilde\sigma = 1.3\) (zoomable)

\(\tilde\sigma = 1.4\) (zoomable)

\(\tilde\sigma = 1.5\) (zoomable)
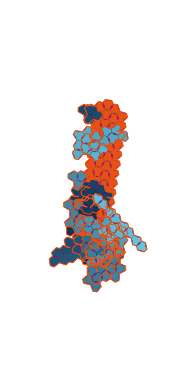
\(\tilde\sigma = 1.6\) (zoomable)

\(\tilde\sigma = 1.7\) (zoomable)
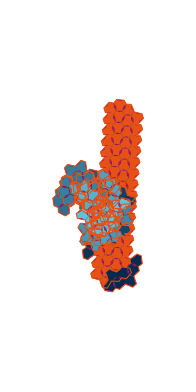
\(\tilde\sigma = 1.8\) (zoomable)

\(\tilde\sigma = 1.9\) (zoomable)

\(\tilde\sigma = 2.0\) (zoomable)

\(\tilde\sigma = 2.1\) (zoomable)

\(\tilde\sigma = 2.2\) (zoomable)

\(\tilde\sigma = 2.3\) (zoomable)

\(\tilde\sigma = 2.4\) (zoomable)

\(\tilde\sigma = 2.5\) (zoomable)

\(\tilde\sigma = 2.6\) (zoomable)

\(\tilde\sigma = 2.7\) (zoomable)

\(\tilde\sigma = 2.8\) (zoomable)

\(\tilde\sigma = 2.9\) (zoomable)

\(\tilde\sigma = 1.0\) (zoomable)
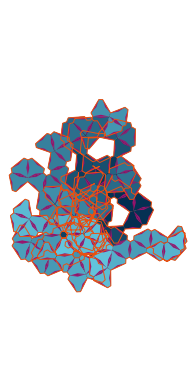
\(\tilde\sigma = 1.1\) (zoomable)
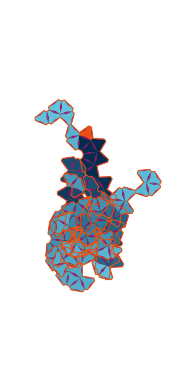
\(\tilde\sigma = 1.2\) (zoomable)
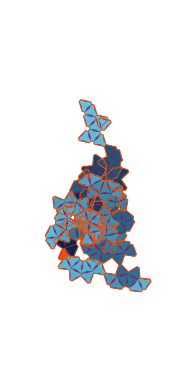
\(\tilde\sigma = 1.3\) (zoomable)

\(\tilde\sigma = 1.4\) (zoomable)

\(\tilde\sigma = 1.5\) (zoomable)

\(\tilde\sigma = 1.6\) (zoomable)

\(\tilde\sigma = 1.7\) (zoomable)

\(\tilde\sigma = 1.8\) (zoomable)

\(\tilde\sigma = 1.9\) (zoomable)
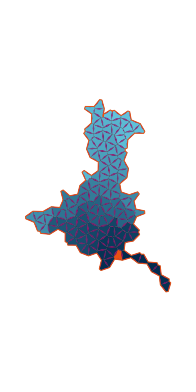
\(\tilde\sigma = 2.0\) (zoomable)
\(\tilde\sigma = 2.1\) (zoomable)

\(\tilde\sigma = 2.2\) (zoomable)

\(\tilde\sigma = 2.3\) (zoomable)
\(\tilde\sigma = 2.4\) (zoomable)

\(\tilde\sigma = 2.5\) (zoomable)
\(\tilde\sigma = 2.6\) (zoomable)

\(\tilde\sigma = 2.7\) (zoomable)

\(\tilde\sigma = 2.8\) (zoomable)

\(\tilde\sigma = 2.9\) (zoomable)

\(\tilde\sigma = 1.0\) (zoomable)

\(\tilde\sigma = 1.1\) (zoomable)

\(\tilde\sigma = 1.2\) (zoomable)

\(\tilde\sigma = 1.3\) (zoomable)

\(\tilde\sigma = 1.4\) (zoomable)

\(\tilde\sigma = 1.5\) (zoomable)

\(\tilde\sigma = 1.6\) (zoomable)

\(\tilde\sigma = 1.7\) (zoomable)

\(\tilde\sigma = 1.8\) (zoomable)

\(\tilde\sigma = 1.9\) (zoomable)

\(\tilde\sigma = 2.0\) (zoomable)

\(\tilde\sigma = 2.1\) (zoomable)
\(\tilde\sigma = 2.2\) (zoomable)

\(\tilde\sigma = 2.3\) (zoomable)

\(\tilde\sigma = 2.4\) (zoomable)

\(\tilde\sigma = 2.5\) (zoomable)

\(\tilde\sigma = 2.6\) (zoomable)

\(\tilde\sigma = 2.7\) (zoomable)

\(\tilde\sigma = 2.8\) (zoomable)

\(\tilde\sigma = 2.9\) (zoomable)
